第5章 循环

    男人至少要擅长一项运动,一种乐器,一种编程，和拿手的几个小炒。

— 《小鸟学AHK》

    男女都一样。

— 大鹏赶紧补充

在我们的生活被阿尔法狗完全接管之前，机器比较适合做重复性的工作。比如你有1000组数据要做线性拟合，比如你有1000张照片文件要加上个拍摄日期，这种操作费时费力并且毫无乐趣，就应该交给机器来解决，这是高效人士的必备技能。本篇就来说说来进行重复工作的基本结构：循环。

5.1 假如没有循环

循环就是兜圈子。先从一个简单例子开始。在练习3.3中，我们做出了一张3行3列的组合图。那时我们还没有学到循环函数，那时的世界过的是这样的苦日子：

mydata2 <- as.data.frame(t(matrix(
  co2, 12, dimnames = list(month.abb, 
                           unique(floor(time(co2)))))))  
mydata2$year <- as.numeric(rownames(mydata2))
x <- mydata2$year
y <- mydata2$Sep
par(mfrow = c(3,3), cex = 1.2, mar = c(3, 2, 0.5, 1))
plot(x = x, y = y, type = 'p')
legend('topleft', legend = 'p', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'l')
legend('topleft', legend = 'l', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'b')
legend('topleft', legend = 'b', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'c')
legend('topleft', legend = 'c', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'o')
legend('topleft', legend = 'o', cex = 0.8,
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'h')
legend('topleft', legend = 'h', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 's')
legend('topleft', legend = 's', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'S')
legend('topleft', legend = 'S', cex = 0.8, 
       bty = "n", text.col = 'blue')
plot(x = x, y = y, type = 'n')
legend('topleft', legend = 'n', cex = 0.8, 
       bty = "n", text.col = 'blue')

虽然是以拷贝粘贴的方式，但也够烦的，不仅无趣，而且容易出错，还浪费纸张，占了本书整整一页纸。都什么时代了，还在用驴拉磨。

经过仔细观察，我们发现，其实每张小图都差不多，除了数据点的类型和图例发生变化外，基本是在重复。这种情况，就可以考虑用循环了。

5.2 循环是个救世主

当循环降临到这个世界上，我们的好日子就来了，上面那段臃肿的代码可以瘦身写成这样：

for (i in c("p", 'l', "b", "c", "o", "h", "s", "S", "n")) {
  plot(x = mydata2$year, y = mydata2$Sep, type = i)
  legend('topleft', legend = i, cex = 0.8, 
         bty = "n", text.col = 'blue')
}

这三句跟上面的十几行语句效果完全等同。i在c("p", 'l', "b", "c", "o", "h", "s", "S", "n")这些字符中按顺序取值走一遭；每走一个值，就执行一次后面方括号里的所有操作。这里出现的for()就是循环语句。

循环就是周而复始，每次的操作都类似，除了for()函数里的i值会发生变化，就像诗里写的：

    究竟
    这一头有几个人能够等你
    下一个轮回翩然来归
    至少我已经不能够
    我的白发，纵有叁千丈怎跟你比长
    下次你路过，人间已无我

— 余光中《欢呼哈雷》

哈雷彗星的运行就是循环，76年一个循环周期。他兜一个圈子回来，我（i）的值已经变了……

虽然写循环语句的时候要多费点脑子，但代码看上去简洁很多，最重要的是修改起来容易，比如我们写完代码后悔了，想把所有的线都改成点，那么循环语句里改一次就行了，不用逐条修改，而且不容易遗漏出错。循环次数越多，写循环语句就越划算。高效人士的又一大福音啊！

i走的那个圈，可以是字符，也可以是别的，比如数字：

for (i in 1:20) print(i)

由于每走一圈只需执行一条语句，所以花括号就省略了。

到目前为止，R 中所有的括号都闪亮登场了一遍，小贴士5.1总结了三种括号在R里扮演的角色。

小贴士 5.1 R语言里的三种括号

  • 圆括号 ()。用作函数和数学表达式，如 mean(x), (1 + 2) * 3。

  • 方括号 []。用作下标，也就是：(1) 调用向量中的某个元素，如x[3], pm[2,6]，以及(2)公式expression()里的下标。

  • 花括号 {}。用作组合，把一组指令组合在一起，如for () {}。

Example 5.1 用print() 指令打印 1 到 100 之间的奇数。

R 中常用的循环语句，除了for()之外，还有while()和 repeat()，从逻辑上来说相互之间可以换用，我们这里就不做介绍了。

5.3 人口增长模型

下面我们用循环语句来做一个指数增长模型，再体会一下循环的意义。

指数增长模型，也叫马尔萨斯增长模型，一个函数的增长率与其函数值成比例。举个例子吧19，我们用 N1 表示 2008 年世界总人口 66.8 亿，r 表示人口自然增长率。为简化起见，假定 r 是个常数 0.011，那么在下一年的总人口就是 N2 = N1 + r * N1。我们想看看今后一百年的人口总数。

第一种方法可以是逐年计算，把各年的人口分别存储到不同的变量中：

N1 <- 66.8
r <- 0.011
N2 <- N1 + r * N1
N3 <- N2 + r * N2  
# ...... 如此写99行，就可以写到 N100。
N100 <- N99 + r * N99

第二种方法，逐年计算，用一个向量来存储各年人口总数。

N <- numeric(100)
N[1] <- 66.8
N[2] <- N[1] + r * N[1]
N[3] <- N[2] + r * N[2]  
# ...... 如此写99行，一直写到 N[100]。
N[100] <- N[99] + r * N[99]

第三种方法， 用循环语句计算，用一个向量来存储各年人口数。

N <- numeric(100)
N[1] <- 66.8
for (t in 1:99) N[t + 1] <- N[t] + r * N[t]

对比这三种方法，循环的好处一目了然。

由于数据储存在一个向量里，我们很容易把人口增长曲线画出来。

Y <- seq(2008, length.out = 100)
plot(Y, N)

根据这个模型的预测，哪一年世界人口超过100亿？当然，可以用肉眼在数据里看。这里，我们画一条y = 100的横线，然后运行鼠标定位函数locator()，接着在横线与指数曲线的交点点一下鼠标，按一下Esc键就可以了:

abline(h = 100)
locator(1)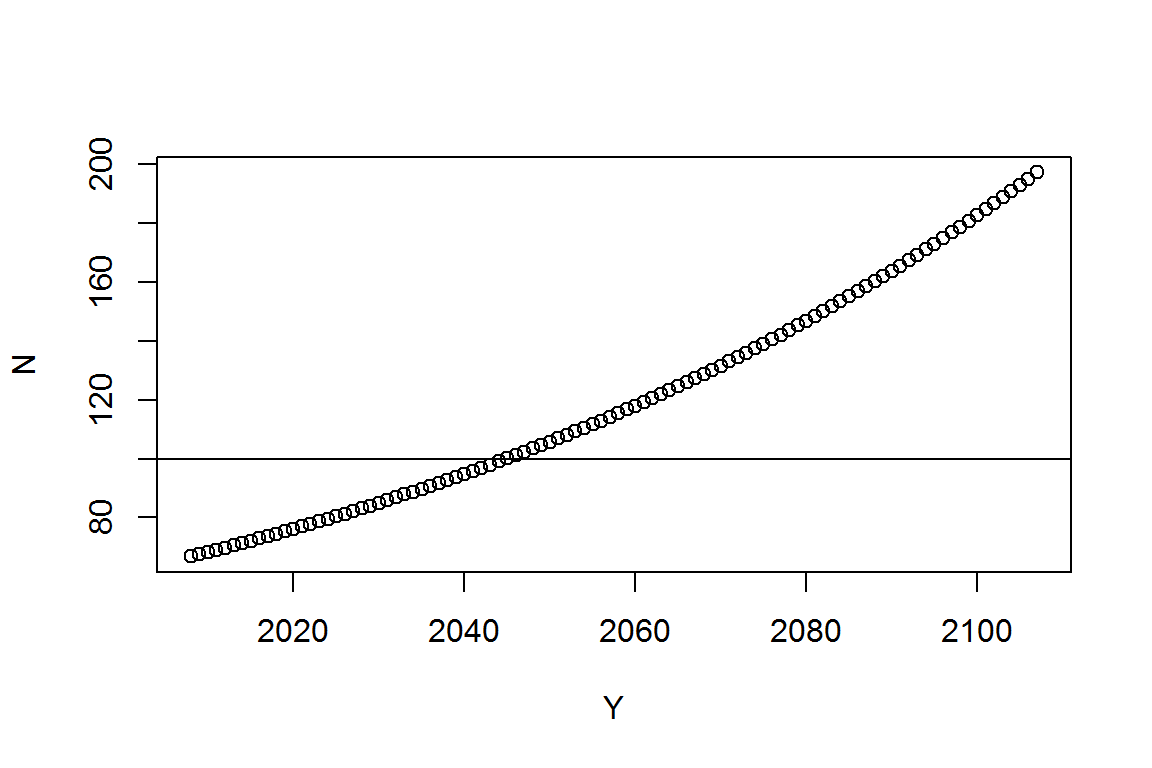
人口增长模型

图 5.1: 人口增长模型

Example 5.2 生成一个矩阵 m （请F1小助理调出matrix()函数的帮助信息），使得 m[i,j] = x[i] * y[j]， 其中 x <- c(2, 3, 5)， y <- c(1, 2, 3, 4)。

5.4 制作动画

动画的原理，其实就是把多幅静态的图片连续播放。根据这个原理，我们在循环中使用plot()画图，相邻两图之间有少许变化，连起来就是一幅动画,例如：

for (i in 1:360) {
    plot(1, ann = F, type = "n", axes = F)
    text(1, 1, "Ninja, go!", srt = i, col =
        rainbow(360)[i], cex = 7 * i/360)
}

下面，我们用类似的方法，来玩一个科学游戏：康威生命游戏。

游戏的设定是这样的：每个玩家有一个国际象棋棋盘，除了边缘外，每个方格被8个方格包围。每个方格里可以居住一个细胞，假定每个细胞周边养活细胞的资源是有限的。

游戏开始时，由玩家选任意多个方格，每个方格放进去一个活细胞。在下一个时刻，细胞的生死由相邻8个方格中的活细胞数量决定：

  • 当相邻的活细胞多于3时，那么由于僧多粥少，中央的这个细胞就会饿死；

  • 当相邻的活细胞少于2时，中央这个细胞会因太孤单而死；

  • 只有在相邻活细胞数量刚好是2或3时，中央的细胞才会活下去；这种情况下，即使中央原本没有细胞，也会诞生一个新细胞。

所以，这个游戏有趣之处在于，游戏开始时该如何放置细胞，放多少个，才能让尽可能多的细胞存活尽可能长的时间？

我们用R代码来实现这个游戏20。用到的绘图函数是image()，在第3.2节已经牛刀小试了一把，现在我们请F1和example()两位助理来帮个忙深入了解：

example(image)

可见，image()绘制的是颜色网格图。

跟上面的例子类似，我们这回用image() 函数做出静态图片，用循环指令来连续播放。

install.packages('simecol')
require(simecol)
# 40 * 40的棋盘:
m <- matrix(0, 40, 40)
# 玩家放置细胞的初始条件。0 表示该位置没有细胞，1 表示有细胞：
m[5:35,19:21] <- 1
# 白色表示没有细胞，绿色有细胞：
image(m, col=c("white", "darkgreen"), axes=FALSE)
for (i in 1:200) {
  nn <- eightneighbours(m)
  m.old <- m
  # 当周围有三个细胞时该位置产生细胞：
  m[m.old == 0 & nn == 3] <- 1
  # 当周围细胞少于 2 个（太孤单）或大于 3 个（太拥挤）时，
  # 该位置细胞死亡。
  m[m.old == 1 & (nn < 2 | nn > 3)] <- 0
  image(m, col=c("white", "darkgreen"), axes=FALSE)
  Sys.sleep(0.1)
}

这里，我们使用了simecol扩展包(Petzoldt and Rinke 2007)，是为了使用其中的 eightneighbours()函数。关于扩展包详见第9章。这个函数有什么作用呢？就像旧版windows里的扫雷游戏，每个方格的数字表示周围8个方格里地雷的数量之和，而这个函数就用来计算矩阵的每个元素相邻周围8个元素之和。

游戏很好玩，如何把动画录制下来保存呢？只要在作图前后增加打开和关闭图片的函数就可以了，比如存成png格式的图片：

png(paste("c:/R/data/conway_", 
          formatC(i, width = 2, flag = "0"), ".png", 
          sep = ""), 
    width = 300, height = 300)
image(m, col=c("white", "darkgreen"), axes = FALSE)
dev.off()

进一步用其他软件（如ffmpeg21）把这些图片连接之后保存在一个文件里，就可以得到一个动画文件。

思考 5.1 所谓失之毫厘，谬以千里。如何用康威生命游戏来模拟蝴蝶效应？当初始条件只改变了一点点，结果会有多大的不同？

R还可以制作3D立体动画。比如，我们可以使用rgl扩展包(Adler, Murdoch, and others 2017)，绘制一个能旋转的带数据点的三维坐标系。

install.packages('rgl')
require(rgl)
example(movie3d)

5.5 超越循环

循环曾经是我们的救世主，但是当我们觉醒之后，却将会试图超越他，因为我们拥有了两种更强大的力量：向量计算和因子计算。

R语言的精华思想之一，是用向量计算来替代循环，提高效率。向量计算的例子早在第1章就出现过了。如果你还记得，我们曾经给x向量里每个元素加了100：

x <- c(61, 45, 55, 46, 56, 79, 86, 57, 56, 56, 57, 71)
x + 100

其中隐藏的逻辑等同于对x的所有元素循环操作一遍:

for (i in 1:12) print(x[i] + 100)

又如第2章遇到过的rowMeans()，rowSums()，diff()等函数，都可以在形式上转换成循环计算。

Example 5.3 第2章里，我们计算mydata2的各列平均值用的是向量计算函数： colMeans(mydata2[, 2:13])。请改写成循环语句，每次求一列的平均值，循环12次。体会循环与向量计算的联系和区别。

再如，第3课作出的图3.18和图3.19，每幅图里边都有多条曲线，如果不使用扩展包ggplot2和lattice，那么就得像本章开头的例子那样逐个画出来，或者用循环语句。而使用了这两个扩展包后，一条语句就画出来了。这得益于作图之前对数据分了组，每组分别作图。而用来分组分类的变量，就是因子（factor）。因子的存在，使得很多计算变得简单轻松了。

这里，我们继续用R自带的数据WorldPhone，来简单介绍一下因子。

这个数据原来的格式中不含有因子，我们调整一下格式，生成mydata3，内容跟原来没有差别，只是变成了列数为3的数据框，三列依次是电话数量、年份、洲名：

wp <- as.data.frame(WorldPhones) # 转化为数据框类型
wp$year <- as.numeric(rownames(wp)) # 将行名称转化为数值类型
mydata3 <- data.frame( # 生成一个新数据框
  nphone = unlist(wp[, 1:7]), year = rep(wp$year, 7),
  conti = rep(names(wp)[1:7], each = nrow(wp)))

mydata3$nphone有 49个数值，可以按年份分成 7 组，也可以按洲名分成7组，这个分组信息就是因子：

summary(mydata3)
##      nphone           year           conti  
##  Min.   :   89   Min.   :1951   Africa  :7  
##  1st Qu.: 1769   1st Qu.:1956   Asia    :7  
##  Median : 3000   Median :1958   Europe  :7  
##  Mean   :16435   Mean   :1957   Mid.Amer:7  
##  3rd Qu.:29990   3rd Qu.:1960   N.Amer  :7  
##  Max.   :79831   Max.   :1961   Oceania :7  
##                                 S.Amer  :7
str(mydata3)
## 'data.frame':    49 obs. of  3 variables:
##  $ nphone: num  45939 60423 64721 68484 71799 ...
##  $ year  : num  1951 1956 1957 1958 1959 ...
##  $ conti : Factor w/ 7 levels "Africa","Asia",..: 5 5 5 5 5 5 5 3 3 3 ...

str()函数用来查看数据的结构，返回的结果告诉我们，mydata3前两列是数字型，第三列是因子型。由于我们打算把年份这一列也作为对nphone这一列的分组信息，那么就需要用as.factor()函数把year这一列转换成因子型：

mydata3$year <- as.factor(mydata3$year)
str(mydata3)
## 'data.frame':    49 obs. of  3 variables:
##  $ nphone: num  45939 60423 64721 68484 71799 ...
##  $ year  : Factor w/ 7 levels "1951","1956",..: 1 2 3 4 5 6 7 1 2 3 ...
##  $ conti : Factor w/ 7 levels "Africa","Asia",..: 5 5 5 5 5 5 5 3 3 3 ...

好了，现在，mydata3$year 也是个因子了。因子的取值叫做“水平” (level)。看看因子有几个水平，水平分别是什么：

nlevels(mydata3$year)
## [1] 7
levels(mydata3$year)
## [1] "1951" "1956" "1957" "1958" "1959" "1960" "1961"
nlevels(mydata3$conti)
## [1] 7
levels(mydata3$conti)
## [1] "Africa"   "Asia"     "Europe"   "Mid.Amer" "N.Amer"  
## [6] "Oceania"  "S.Amer"
Example 5.4 以电话数量为y，年份为因子，做出箱型图boxplot()。如果以洲为因子呢？

因子有什么用呢？既然因子就是分类变量，那么用处当然就是用来对数据分类了。请看下面的例子：

如果我们要计算mydata3每年这几大洲的电话总和，可以利用循环函数，对每个年份因子依次计算。

for (i in levels(mydata3$year)) {
  print(sum(mydata3$nphone[mydata3$year == i]))
}
## [1] 74494
## [1] 102199
## [1] 110001
## [1] 118399
## [1] 124801
## [1] 133709
## [1] 141700

虽然能算出结果，但逐个计算的效率很低。幸好，我们有tapply()函数（table apply 的缩写）：

tapply(mydata3$nphone, mydata3$year, sum)
##   1951   1956   1957   1958   1959   1960   1961 
##  74494 102199 110001 118399 124801 133709 141700

这样，就很方便地得到了整齐的表格。

tapply()是apply()家族的函数之一。这个家族成员长得很像，脾气秉性却各有不同。我们再挑两个来举例。

前面用过的二氧化碳数据，如果想得到每一列的几个常见统计量，以前我们是这样操作的：

mydata2 <- read.csv(file = "c:/r4r/co2.csv")
smr1 <- summary(mydata2)
smr1

虽然可以把统计量保存在表格里，看起来也算美观，但想取出来里边的数据却比较麻烦，因为全是字符，不是数字。比如我们想计算这几十年的所有1月份数据里最大值（smr1[6, 2]）与最小值（smr1[1, 2]）的差，也就是极差，那么下面的计算是不行的：

smr1[6, 2] - smr1[1, 2]
## Error in smr1[6, 2] - smr1[1, 2]: 
##  non-numeric argument to binary operator

我们将来在第10章会学到，字符型变量是不能做数学运算的。那么，如果想调用summary()得到的数据做后续计算该怎么办？用lapply()或sapply()函数：

smr2 <- lapply(mydata2, summary)
smr2[[2]][6] - smr2[[2]][1]

smr3 <- sapply(mydata2, summary)
smr3[6, 2] - smr3[1, 2]

lapply()返回的值是个列表（list），我们将来会择吉日在第8.1节介绍；而sapply()返回的是个我们熟悉的数据框。这样，就可以进行后续计算了。

除了apply(), tapply(), lapply(), sapply(), 这个家族还包括rapply(), vapply()，mapply()等。他们让很多原本需要循环才能完成的计算都变成了轻松爽快的向量计算。这里我们略过不表，感兴趣的话就找F1和example()两位助理吧。

很多函数对因子青睐有加，遇见因子就会做特殊考虑。比如第3.5节提到的ggplot2和lattice扩展包。再如，plot()函数如果遇到了因子，就会呈现第五种化身（图5.2）：

plot(x = mydata3$year, y = mydata3$nphone)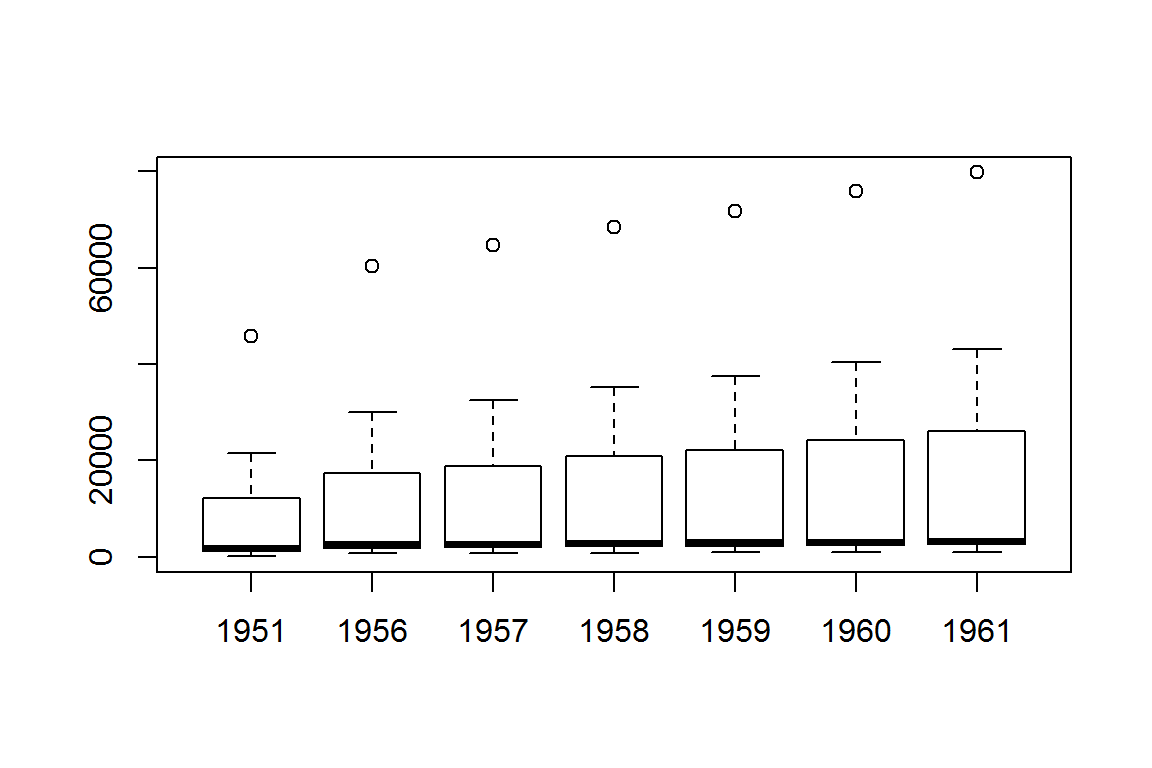
当plot()遇见因子.

图 5.2: 当plot()遇见因子.

由于x是用来分组的因子，plot()认为我们是要查看每组数据的分布情况，就自动化身为箱型图。等同于

boxplot(mydata3$nphone ~ mydata3$year)

利用向量计算来代替循环，虽然运算效率高，但对新手来说，脑子需要多绕两个弯。如果不习惯，那么，继续使用循环也没有什么不妥。还记得我们的入门第二秘诀吗？

    能用就行！
Example 5.5 用tapply()和示例数据，分别计算各年几大洲的电话数量的最大值、最小值、中值。

5.6 课外活动：信息提示

有些循环比较耗时。比如，在对大量数据作成百上千张复杂的图形时，可能每张图都要耗时几秒钟，那么完成所有工作就需要几十分钟。在等待的过程中，让R适当地给个进度提示，会比较有助于估算剩余的时间。

如果想提示进度，最简单的是在代码里加入print()函数，正如我们在人口曲线中所用的代码一样。我们也可以让操作系统弹出对话框来提示。下面这个例子，我们用winDialog()函数，在每计算完1个年份的人口数量时，就将循环暂停，弹出个对话框，直到你关闭之后才计算下一个年份。

N <- numeric(100)
N[1] <- 66.8
r <- 0.011
for(t in 1:3)
{
  N[t+1] <- N[t] + r * N[t]
  winDialog(type = c("ok"), 
            message = paste('population in',t + 2007, 
                            'will be', N[t+1])) #信息提示框
}

当然，我们也可以把winDialog()放在一段代码的结尾，运行之后就可以放手去做别的事情，直到听到信息提示音，就知道R把工作做完了（我们将在第13.2节演示这样一个例子）。

winDialog()连同我们前边见过的file.choose()函数一样，都属于R与用户交互对话的函数。这样的函数常见的还有winDialogString()，用来让用户在弹出的窗口输入文字并返回R：

n <- winDialogString(
  message = "which year's population would you like to see", 
  default = '2050')
winDialog(type = c("ok"), message = paste(
  'population in', n, 'will be', N[as.numeric(n) - 2007]))

上面这个例子里，第一行用来让用户输入个年份，第二行把该年的预测人口数以对话框的形式弹出来。当然，这两行可以合成1句：

winDialog(type = c("ok"), message = paste(
  'population in', winDialogString(
    message = "which year's population would you like to see",
    default = '2050'), 'will be', N[as.numeric(n) - 2007]))

采用这样的方法，就实现了用户和R的交互对话。

References

Petzoldt, Thomas, and Karsten Rinke. 2007. “Simecol: An Object-Oriented Framework for Ecological Modeling in R.” Journal of Statistical Software 22 (9): 1–31. http://www.jstatsoft.org/v22/i09.

Adler, Daniel, Duncan Murdoch, and others. 2017. Rgl: 3D Visualization Using Opengl. https://CRAN.R-project.org/package=rgl.

  1. 本例来自Björn Reineking 教授 Introduction to R 课程讲义。↩

  2. 本例来自Björn Reineking 教授 Introduction to R 课程讲义。↩

  3. ffmpeg：https://ffmpeg.org/↩