第6章 分支

    日出日落，月圆月缺，年尾年头，这是“循环”；
    上学还是就业，单身还是结婚，丁克还是生娃，这是“分支”；
    不管是循环还是分支，都嵌入在生老病死的时间轴上，这是“顺序”。
    所谓尽人事听天命，想来就是心平气和地接受顺序结构，小心翼翼地制订循环结构，在关键时刻控制好分支结构，就这样度过一生罢。

—大鹏志22

顺序、循环和分支是编程的三大结构。顺序最简单，就是运行完第一行接着运行第二行；上一章我们学习了循环；这一章说说分支。

什么是分支？分支就是你到了一个路口，向左向右向前看，要选择到底往哪个方向走。每时每刻我们都要做出选择：渴了，是喝咖啡还是茶？见了人，是上去打招呼还是悄悄躲开？这本书读到这里，是扔掉还是继续读下去？这都是分支。

简单来说，分支就是先判断再选择。而所谓判断，就是逻辑运算。

6.1 判断：逻辑运算

关于逻辑运算，让我们先来做一套健脑操热热身：

3 > 2  # 3比2大？是真（true）的。
## [1] TRUE
1 > 2  # 1比2大？是假（false）的。
## [1] FALSE
!(1 > 2)  # 1不比2大？呃......
## [1] TRUE
3 > 2 & 1 > 2  # 3比2大，并且1比2大？假的。
## [1] FALSE
3 > 2 | 1 > 2  # 3比2大，或者1比2大吗？真的。
## [1] TRUE
3 > 2 & !(1 > 2)  # 3比2大，并且1不比2大？好像是真的吧......
## [1] TRUE

好了，热身完毕。包括上面出现的，常用的逻辑运算符有：大于>， 小于<，等于==，不等于!=，小于或等于 <=，大于或等于>=， 与&，非!， 或|。

逻辑运算符用在向量上，得到的结果也是向量：

x <- 1:3
x == 2
## [1] FALSE  TRUE FALSE
x == 2 | x == 3
## [1] FALSE  TRUE  TRUE
y <- c(4, 1, 2)
x > y
## [1] FALSE  TRUE  TRUE
x > y & y > 1
## [1] FALSE FALSE  TRUE

逻辑运算的结果，也就是TRUE和FALSE，相当于数字的1和0，可以做数学运算：

TRUE * FALSE
## [1] 0
TRUE + TRUE
## [1] 2

这意味着，既然上面最后一个例子x > y的返回值是逻辑值FALSE, TRUE, TRUE，那么我们可以对这个逻辑值用sum()函数求总和，得到的就是“x里总共有多少个元素大于y”：

sum(x > y)
## [1] 2
思考 6.1 除了加减法，逻辑值TRUE和FALSE还能参与哪些运算？逻辑值能否参与“比大小”和“与非或”的逻辑运算？

Example 6.1 设 m <- 6:1，n <- c(3, 5, 6)，判断 m 中的每个元素是否在n中出现。

Example 6.2 从 1:100 中挑出既能被 2 整除，又能被 3 整除的数。

Example 6.3 从1到10000中，挑出所有的素数。

上面这些练习，可以用循环来完成。不过，由于R很照顾追求高效的人士，对于像练习6.1这样的任务，R提供了更方便的方法：

x %in% y
## [1]  TRUE  TRUE FALSE

得到的结果依次是x向量里的三个元素是否在y中出现。

如果逻辑值出现在下标里边，那么R就会把TRUE对应的下标挑出来。结合逻辑判断和下标系统，就可以挑出 x 中哪些元素出现在 y 中，以及出现的位置：

x[x %in% y]
## [1] 1 2
which(x %in% y)
## [1] 1 2

上一课提到了马尔萨斯增长模型，我们用鼠标取点的方式，找出了哪一年世界人口超过100亿。现在有了逻辑判断，完成这个任务就更容易更准确了：

Y[N > 100][1]
Example 6.4 在练习1.2中，我们曾经提出个问题：PM2.5 一天中的最大值出现在几点钟？请用逻辑判断运算来回答。

Example 6.5 世界卫生组织制订的 PM2.5 指导标准中最宽松的标准是24小时均值75微克每立方米。请在上题数据中挑出北京一天内超出此标准的时段。

上面讲的是分支两部曲的第一步：判断。下面说说第二步：选择。

6.2 选择：如果，那么，否则

分支语句的最简单结构，用人类语言表达就是：

如果饿了，那么就吃。

将人类语言翻译成R语言就是：

if (饿了) {吃}

跟循环语句类似，如果只有“吃”这一个动作，那么花括号{}可以不写。当发生一系列动作时，就需要全部放进花括号里，并且为了看上去清楚，一般会添加一些换行符。下面是几个实例。

x <- 60
# 如果x小于75，那么在显示区打印出来一句话：
if (x < 75) print("x is less than 75")  
## [1] "x is less than 75"
if (x < 75) {
    print("x is less than 75")
    y <- x + 10
    print(y)
    }
## [1] "x is less than 75"
## [1] 70

复杂一点的判断，就是后面加上了“否则”：

如果饿了，那么就吃；否则，就干活儿。

翻译成R语言，就是：

if (饿了) {吃} else {干活儿}

具体用起来是这样的：

x<- 60
if (x < 75) {
    print("x is less than 75")
} else {
    print("x is larger than 75")
}  # 如果()，那么{}，否则{}。
## [1] "x is less than 75"

无论是循环语句还是条件语句，都可以像俄罗斯套娃那样，一层套一层，大壳套小壳，比如说：

如果饿了，那么就吃和喝；否则，如果困了，那么就睡；否则，就干活儿。

翻译成R语言就是：

if (饿了) {吃} elseif (困了) {睡} else {干活儿}

继续上面的例子：

x <- 60
if (x < 75) {
    print("small")
} else if (x > 90){
    print("large")
} else {
    print("good")
}
## [1] "small"

这样写起来显得啰嗦，于是有了瘦身版ifelse()函数。

ifelse(x < 75, "small", "large")

效果等同于上一个例子。不同的是，这里 x 的向量长度可以大于1。比如，试试 x <- 60:100。

ifelse()函数也可以嵌套，像这样：

ifelse(x < 75, "small", ifelse(x > 90, "large", "good"))
## [1] "small"

如果嵌套太多，ifelse()函数也会显得啰嗦，那么可以适当考虑进一步的瘦身版——switch()函数，详见F1小助理。

思考 6.2 if () {} else {}、ifelse()、switch()，这三个函数之间，何时能相互替换，何时不能？

有了分支语句，就可以在很多地方派上用场了。比如，继续以马尔萨斯人口增长模型的数据作图，把超过100亿的数据点用红色区分出来：

N <- numeric(100)
N[1] <- 66.8
for (t in 1:99) N[t + 1] <- N[t] + r * N[t]
Y <- seq(2008, length.out = 100)
plot(x = Y + 2007, y = N, xlab = "Year", ylab = "Population", 
     cex = ifelse(N >= 100, 2, 1), pch = 16, type = "b", 
     col = ifelse(N >= 100, "red", "darkgreen"))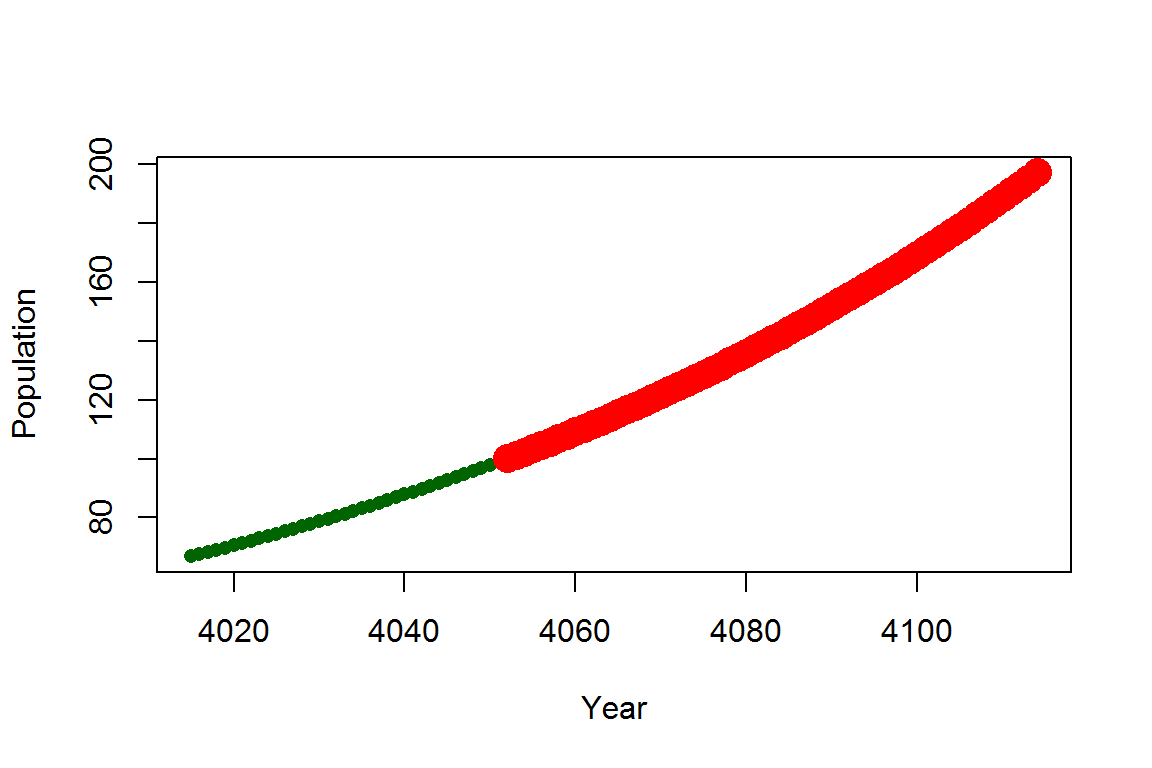
用分支函数给数据点涂上不同颜色.

图 6.1: 用分支函数给数据点涂上不同颜色.

6.3 课外活动：复活节

我们都知道，“计算机”一词在英文称为 computer，而compute 和 computation 分别是动词和名词的“计算”，他们均来自拉丁语的Computus，而这个词的本意是“计算复活节的方法”。作为欧美国家最重要的节日之一，复活节，竟然难以计算是日历上的哪一天；复活节的计算，自古就是在考验人类的计算水平。今天，就让我们用R来试试计算每年的复活节是在日历的哪一天。

复活节用来纪念耶稣基督被钉死后复活。根据定义，复活节是每年春分月圆之后第一个星期日。为什么这样规定呢？据说，春分后北半球开始日长夜短，所以春分意味着光明的到来；月圆时夜晚也洒满光辉，同样意味着光明的到来。耶稣在光明到来的这一天复活，那么耶稣便是光明的使者。而星期日，是因为上帝星期天休息，我们也不上班，在家过节。

由于基督教有三大主要派别，其中天主教和基督新教（华语圈常简称基督教）属于西方罗马教会，使用公历；东正教属于东方教会，使用儒略历。每种历法中，又存在不同的计算方法23。

第一种是数学王子高斯提出的高氏算法：

用Y表示年份，mod表示整除的余数（例如13 mod 5 = 3）。那么：

  • a = Y mod 19
  • b = Y mod 4
  • c = Y mod 7
  • d = (19a + M) mod 30
  • e = (2b + 4c + 6d + N) mod 7

其中，M和N的取值，在东正教会的儒略历M=15,N=6，而西方教会所用的公历的取法参见下表：

年份 M N
1583-1699 22 2
1700-1799 23 3
1800-1899 23 4
1900-2099 24 5
2100-2199 24 6
2200-2299 25 0
  • 若d+e < 10则复活节在3月(d+e+22)日，反则在4月(d+e-9)日，除了两个特殊情况：
  • 若公式算出的日期是4月26日，复活节在4月19日；
  • 若公式算出的日期是4月25日，同时d=28、e=6和a>10，复活节应在4月18日。

第二种是米氏（Meeus）算法。在公历中，

  • a = Y mod 19
  • b = Y / 100
  • c = Y mod 100
  • d = b / 4
  • e = b mod 4
  • f = (b + 8) / 25
  • g = (b - f + 1) / 3
  • h = (19a + b - d - g + 15) mod 30
  • i = c / 4
  • k = c mod 4
  • l = (32 + 2 * e + 2 * i - h - k) mod 7
  • m = (a + 11 * h + 22 * l) / 451
  • month = (h + l - 7 * m + 114) / 31
  • day = ((h + l - 7 * m + 114) mod 31) + 1

在儒略历中，

  • a = Y mod 4
  • b = Y mod 7
  • c = Y mod 19
  • d = (19c + 15) mod 30
  • e = (2a + 4b - d + 34) mod 7
  • 月 = (d+e+114) / 31
  • 日 = ((d+e+114) mod 31) + 1

请把上面的算法用R代码写出来，并计算最近十年的复活节在几月几日。高氏算法和米氏算法的结果有差别吗？

  1. 大鹏志：http://dapengde.com↩

  2. 算法来自维基百科。↩